Kommenteissa on käyty hieman keskustelua, onko havaintoni tosi, että kuukauden viimeinen päivä on yleensä kalliimpi kuin kuukauden muut päivät. Löysin itselleni riittävän varmistuksen, että ilmiö esiintyy, mutta harvinaisempana kuin luulin.
Jätän sovinnolla tilastomatemaatikoille täydellisen analyysin siitä, onko jokin asia tilastollisesti merkittävä – niin kuin useimpien tiedemiestenkin pitäisi jättää. Asia on sen verran monimutkainen eikä siitä tilastotieteilijätkään tunnu aina olevan samaa mieltä.
Asiaa monimutkaistaa se, että kuukauden viimeinen päivä on joskus viikonloppupäivä. Viimeinen päivä pitäisi normalisoida kuukauden keskiarvoa vastaavaksi päivähinnaksi ottaen huomioon viikonpäivä. Olen tässä vetänyt hieman mutkia suoriksi tältä osin, vaikka tiedot viikonloppuhintojen suhteesta arkihintaan olisi saatavissa omista tilastoistani. Niiden kaivaminen jää seuraavan kerran aktiivisuuden varaan.
Ensinnäkin olen laskenut vuosien 2012, 2013 ja 2014 alun jokaisen kuukauden keskiarvon ja keskihajonnan. Tämä tarkoittaa sitä, että kuukauden hintojen oletetaan asettuvan normaalijakauman ”kellokäyrälle” kuukausikeskiarvon ympärille. Keskihajonta kertoo kellokäyrän leveyden.
Käytännön ilmiöillä on taipumus asettua kellokäyrän muotoon havaintojen keskiarvon ympärille. Keskiarvohintoja on eniten kellokäyrän huipun kohdalla. Mitä kauemmaksi keskiarvosta mennään, sen epätodennäköisempää kyseinen hinta on. Kellokäyrä on aina samanmuotoinen, joten kun tiedämme keskiarvon ja keskihajonnan, voimme laskea tarkan arvon jonkun hinnan todennäköisyydelle. Parhaan kuvan jonkin hinnan todennäköisyydestä saamme, jos laskemme, kuinka todennäköistä on, että hinta on noin korkea tai vielä korkeampi.
Esimerkiksi vuoden 2012 tammikuussa sähkö maksoi keskimäärin 3,88 c/kWh. Keskihajonta oli 0,64 c/kWh, mikä on melko keskimääräinen hajonta vuonna 2012. Tämä hajonta kuvaa kellokäyrän leveyttä (mutta ei kovin helposti kuvattavalla tavalla). Tammikuun viimeisen päivän sähkön hinta oli 5,5 c/kWh. Tämä hinta on selvästi kaukana keskiarvosta. Esimerkiksi taulukkolaskimista löytyvä funktio NORMDIST (tai NORM.JAKAUMA) kertoo näppärästi, että tammikuun sähkönjakaumalla näin korkean päivähinnan esiintymisen todennäköisyys tällaisen tammikuun tiettynä päivänä on vain 0,6% eli noin kerran kahdesta sadasta.
Tilastollisen merkittävyyden havaitseminen on hankalaa, mutta usein käytetään hihasta vedettyä arvoa p=0,95. Tämä tarkoittaa sitä, että jos toteamme tapahtuvaksi jotain, jonka todennäköisyys satunnaisessa prosessissa olisi alle yksi kahdestakymmenestä, meillä on lupa pitää tapausta vähintäänkin omituisena. Mutta vain, jos aineistomme on tarpeeksi kattava.
Katsopaanpa sitten raakatietoa, miten viimeisen päivän hinta on osunut kunkin kuukauden kellokäyrälle. Todennäköisyys 50% tarkoittaa sitä, että viimeisen päivän hinta on täsmälleen kuukauden keskiarvo. Lähellä nollaaa oleva todennäköisyys tarkoittaa nousua, jonka todennäköisyys on pieni. 50% – 100% olevat todennäköisyydet tarkoittavat keskiarvoa pienempiä hintoja, lähellä 100% olevat ovat yllättäviä hinnanlaskuja viimeiseksi päiväksi.
|
|
keskiarvo c/kWh |
keskihajonta c/kWh |
viim. päivä c/kWh |
todennäköisyys |
| 2012 |
|
|
|
|
|
|
tammikuu |
3,88 |
0,64 |
5,50 |
0,6% |
|
helmikuu |
5,28 |
2,11 |
3,55 |
79,4% |
|
maaliskuu |
3,65 |
0,64 |
3,17 |
77,2% |
|
huhtikuu |
3,65 |
0,66 |
2,89 |
87,5% |
|
toukokuu |
3,33 |
0,63 |
4,41 |
4,6% |
|
kesäkuu |
2,74 |
0,55 |
2,26 |
80,8% |
|
heinäkuu |
1,37 |
0,65 |
1,83 |
23,7% |
|
elokuu |
3,82 |
1,10 |
4,22 |
36,0% |
|
syyskuu |
4,10 |
0,65 |
2,77 |
98,0% |
|
lokakuu |
3,86 |
0,38 |
4,06 |
29,6% |
|
marraskuu |
3,69 |
0,42 |
4,50 |
2,7% |
|
joulukuu |
4,68 |
1,30 |
3,30 |
85,6% |
| 2013 |
|
|
|
|
|
|
tammikuu |
4,16 |
0,66 |
3,55 |
82,1% |
|
helmikuu |
3,94 |
0,22 |
3,99 |
41,9% |
|
maaliskuu |
4,50 |
0,43 |
4,45 |
54,7% |
|
huhtikuu |
4,29 |
0,82 |
3,66 |
81,6% |
|
toukokuu |
3,73 |
0,36 |
3,99 |
24,4% |
|
kesäkuu |
3,86 |
0,96 |
2,66 |
89,5% |
|
heinäkuu |
3,70 |
0,32 |
3,69 |
51,2% |
|
elokuu |
4,35 |
0,65 |
3,69 |
84,3% |
|
syyskuu |
4,78 |
0,84 |
4,61 |
58,0% |
|
lokakuu |
4,60 |
1,11 |
4,29 |
61,0% |
|
marraskuu |
3,80 |
0,34 |
3,64 |
68,5% |
|
joulukuu |
3,56 |
0,73 |
3,02 |
77,3% |
| 2014 |
|
|
|
|
|
|
tammikuu |
4,02 |
0,68 |
4,46 |
25,8% |
|
helmikuu |
3,42 |
0,40 |
3,61 |
31,2% |
|
maaliskuu |
3,12 |
0,44 |
4,00 |
2,4% |
|
huhtikuu |
3,13 |
0,49 |
3,01 |
60,3% |
Kirkkaan punaiset ovat hinnanousuja, joiden todennäköisyys on alle kerran kahdestakymmenestä. Vaalean punaiset ovat pienempiä hinnanousuja. Vihreät ovat kuukausia, joina viimeisen päivän hinta on matalampi, kuin kuukauden keskiarvo. Kirkkaanvihreän hinnanlaskun todennäköisyys on vain viisi prosenttia.
Olemme löytäneet neljä hinnannousua, joiden todennäköisyys on vain yksi kahdestakymmenestä. Kuukausia on 28, joten tällaisia hinnannousuja pitäisi olla tilastollisesti vain 1-2. Hinnanlaskuja on yksi, kuten tilastollisesti pitäisikin olla.
Mutta edellisessä laskelmassa on yksi olennainen virhe. Eri viikonpäivinä, erityisesti viikonloppuisin on tyypillisesti eri hinnat. Jos kuukauden viimeiseksi päiväksi sattuu lauantai tai sunnuntai (todennäköisyys 2/7 eli 29%), on aivan luonnollista, että tuona kuukautena viimeisen päivän hinta laskee. Jotta voimme vertailla viimeisen päivän hintaa kuukausihintaan, meidän pitäisi hieman korjata sitä kyseisen kuukauden tyypillisen arki/viikonloppusuhteen perusteella. Arkipäivän hintaa pitäisi hieman laskea ollakseen kuukausihinnan kanssa verrannollinen, koska tietty osa kuukauden päivistä on ollut joka tapauksessa viikonloppuja.
Olen laskenut viikonloppujen ja arkipäivien suhteet, mutta olin tällä kertaa liian laiska kerätäkseni niitä kaikkia. Vain vuoden 2014 luvut ovat tarkkoja kuukausikeskiarvo / arkikeskiarvo (vappuaatto viikonlopun mukaan). Käytän tässä viikonloppupäiville huhtikuun 2014 kerrointa 1,2 saadakseni ne vertailukelpoisiksi kuukausihinnan kanssa, ja arkipäiville kerrointa 0,95. Uudenvuodenaatto on saanut viikonloppukertoimen 1,2 ja vappuatto kertoimen 1,1. Maaliskuun viimeiseksi 2013 sattunut pääsiäissunnuntai on saanut kertoimen 1,3. Nuo kertoimet eivät kovin paljoa eroa todellisista ja todennäköisillä tarkoilla arvoilla päädymme samaan lopputulokseen.
Tällä tavalla korjattuna päädymme seuraavaan taulukkoon:
|
|
keskiarvo c/kWh |
keskihajonta c/kWh |
viim. päivä c/kWh |
todennäköisyys |
todennäköisyyksien keskiarvo |
viim. p. |
kerroin |
korjattu todennäköisyys |
todennäköisyyksien keskiarvo |
| 2012 |
|
|
|
|
|
50,5% |
|
|
|
44,6% |
|
tammikuu |
3,88 |
0,64 |
5,50 |
0,6% |
|
ti |
0,95 |
1,8% |
|
|
helmikuu |
5,28 |
2,11 |
3,55 |
79,4% |
|
ke |
0,95 |
81,7% |
|
|
maaliskuu |
3,65 |
0,64 |
3,17 |
77,2% |
|
la |
1,20 |
40,5% |
|
|
huhtikuu |
3,65 |
0,66 |
2,89 |
87,5% |
|
ma* |
1,20 |
61,0% |
|
|
toukokuu |
3,33 |
0,63 |
4,41 |
4,6% |
|
to |
0,95 |
9,0% |
|
|
kesäkuu |
2,74 |
0,55 |
2,26 |
80,8% |
|
la |
1,20 |
52,2% |
|
|
heinäkuu |
1,37 |
0,65 |
1,83 |
23,7% |
|
ti |
0,95 |
28,3% |
|
|
elokuu |
3,82 |
1,10 |
4,22 |
36,0% |
|
pe |
0,95 |
43,3% |
|
|
syyskuu |
4,10 |
0,65 |
2,77 |
98,0% |
|
su |
1,20 |
88,4% |
|
|
lokakuu |
3,86 |
0,38 |
4,06 |
29,6% |
|
ke |
0,95 |
49,9% |
|
|
marraskuu |
3,69 |
0,42 |
4,50 |
2,7% |
|
pe |
0,95 |
8,3% |
|
|
joulukuu |
4,68 |
1,30 |
3,30 |
85,6% |
|
ma* |
1,20 |
71,0% |
|
| 2013 |
|
|
|
|
|
64,5% |
|
|
|
53,0% |
|
tammikuu |
4,16 |
0,66 |
3,55 |
82,1% |
|
to |
0,95 |
88,3% |
|
|
helmikuu |
3,94 |
0,22 |
3,99 |
41,9% |
|
to |
0,95 |
76,3% |
|
|
maaliskuu |
4,50 |
0,43 |
4,45 |
54,7% |
|
su* |
1,30 |
0,2% |
|
|
huhtikuu |
4,29 |
0,82 |
3,66 |
81,6% |
|
ti* |
1,20 |
45,3% |
|
|
toukokuu |
3,73 |
0,36 |
3,99 |
24,4% |
|
pe |
0,95 |
44,3% |
|
|
kesäkuu |
3,86 |
0,96 |
2,66 |
89,5% |
|
su |
1,20 |
75,8% |
|
|
heinäkuu |
3,70 |
0,32 |
3,69 |
51,2% |
|
ke |
0,95 |
72,8% |
|
|
elokuu |
4,35 |
0,65 |
3,69 |
84,3% |
|
la |
1,20 |
44,7% |
|
|
syyskuu |
4,78 |
0,84 |
4,61 |
58,0% |
|
ma |
0,95 |
68,4% |
|
|
lokakuu |
4,60 |
1,11 |
4,29 |
61,0% |
|
to |
0,95 |
68,2% |
|
|
marraskuu |
3,80 |
0,34 |
3,64 |
68,5% |
|
la |
1,20 |
4,8% |
|
|
joulukuu |
3,56 |
0,73 |
3,02 |
77,3% |
|
ti* |
1,20 |
46,6% |
|
| 2014 |
|
|
|
|
|
29,9% |
|
|
|
27,8% |
|
tammikuu |
4,02 |
0,68 |
4,46 |
25,8% |
|
pe |
0,92 |
45,2% |
|
|
helmikuu |
3,42 |
0,40 |
3,61 |
31,2% |
|
pe |
0,96 |
44,8% |
|
|
maaliskuu |
3,12 |
0,44 |
4,00 |
2,4% |
|
ma |
0,97 |
4,4% |
|
|
huhtikuu |
3,13 |
0,49 |
3,01 |
60,3% |
|
ke* |
1,20 |
16,7% |
|
(*) Päivä on juhlapyhä tai aatto.
Päädymme neljään kuukauteen 28:sta, joina sähkön hinta kuukauden viimeisenä päivänä on noussut niin voimakkaasti, ettei sen todennäköisyys ole kuin kerran kahdestakymmenestä. Tämä on yli kaksi kertaa enemmän kuin olisi todennäköistä satunnaisaineistolla. Näistä päivistä vain yksi on erikoispäivä (pääsiäissunnuntai), kaksi on tavallisia arkipäiviä ja yksi lauantai. Pääsiäissunnuntaina 2013 olisi yllättävä (<5%) hinnannousu, vaikka se laskettaisiin tavalliseksi sunnuntaiksikin. Kuutena kuukautena hinta on noussut niin paljon, että sen todennäköisyys on yksi kymmenestä. Näitäkin pitäisi olla alle kolme, joten näitäkin on yli kaksinkertainen määrä siihen nähden, mitä satunnaisaineistossa pitäisi olla.
Lopputuloksena saamme kohtuullisen tilastollisen varmuuden, että kuukauden viimeinen päivä on kalliimpi kuin muut päivät. Tosin tämä ilmiö ei ole aivan niin selvä, kuin olisin odottanut. Monena kuukautena viimeisen päivän hintataso on eronnut selvästi sitä edeltävästä hintatasosta, mutta ero kuukauden yleiseen hintatasoon ei ole niin selvä. Tässä aineistossa ei ole myöskään minkäänlaista jälkeä vuosineljänneksen viimeisen päivän kalleudesta verrattuna muiden kuukausien viimeisiin päiviin, minkä olen ollut huomaavinani viime vuonna.
PS. Yksi asia, mikä jäi mietityttämään ensi kertaa varten on, että kellokäyrää laskettaessa mukana on myös viimeisen päivän hinta. Oikeastaan viimeisen päivän omituisuus pitäisi laskea kuukauden muihin päiviin verrattuna eli viimeisen päivän hinnan ei pitäisi olla keskiarvon ja normaalijakauman laskemisessa mukana. Nyt voi käydä niin, että viimeisen päivän hinnanousu lisää keskihajontaa, jonka vuoksi viimeisen päivän hinta muuttuukin ”normaalimmaksi”.
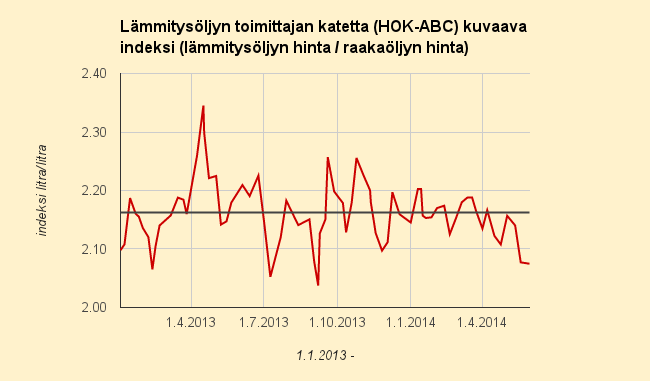
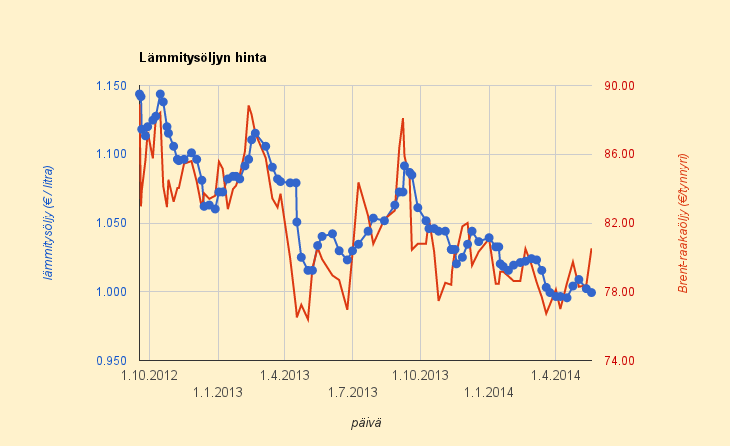
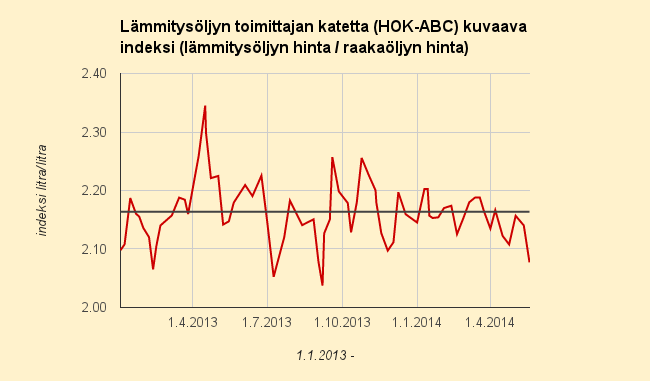
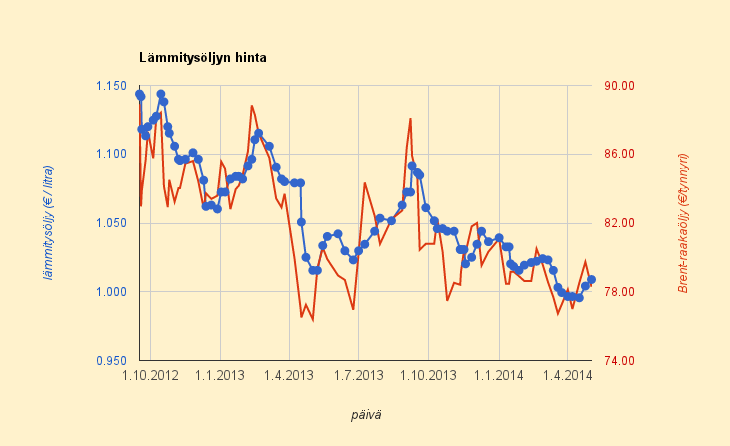
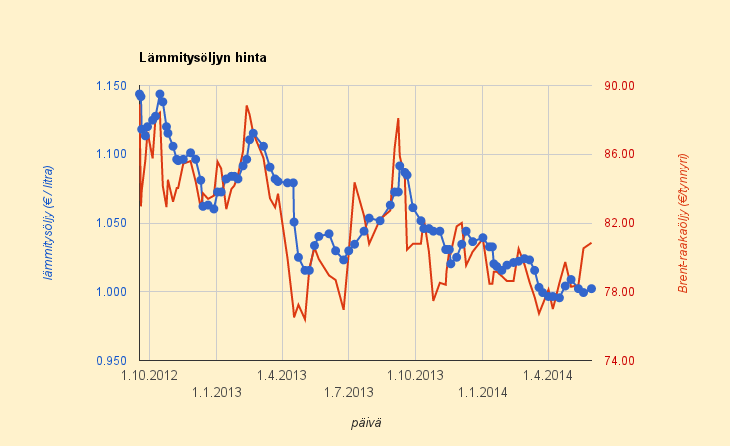 Lämmitysöljyn vertailuhinta (HOK/ABC-5%) pysyi sisukkaasti kaksi viikkoa euron litralta alapuolella raakaöljyn hinnannoususta huolimatta. Hinta 19.5.2014 – 29.5.2014 oli 0,999 €/l ja nyt se nousee tasolle 1,003 €/l. Raakaöljyn hinta euroissa on noussut tänä aikana yli kolme prosenttia.
Lämmitysöljyn vertailuhinta (HOK/ABC-5%) pysyi sisukkaasti kaksi viikkoa euron litralta alapuolella raakaöljyn hinnannoususta huolimatta. Hinta 19.5.2014 – 29.5.2014 oli 0,999 €/l ja nyt se nousee tasolle 1,003 €/l. Raakaöljyn hinta euroissa on noussut tänä aikana yli kolme prosenttia.